Étiquette : hyperespace

Gilles Baroin
Doctorant et Ingénieur, INSA Lyon, Université Toulouse – Jean Jaurès
gilles/@/baroin.org

Pour citer cet article : Baroin, Gilles, « De Newton à Riemann, Graphes et Graphisme : Interactions Mathématico-Musico-Plastiques. », Litter@ Incognita [En ligne], Toulouse : Université Toulouse Jean Jaurès, n°3 « Les Interactions II », 2010, mis en ligne en 2010, disponible sur <https://blogs.univ-tlse2.fr/littera-incognita-2/2018/01/09/la-ville-contemp…ite-au-generique/>.

Télécharger l’article au format PDF

---

Résumé

Sir Isaac Newton, fasciné par l’interaction de la lumière au travers d’un prisme, fut le premier à l’étudier et l’expliquer ; il dessina son cercle chromatique en associant couleurs et notes de musique. Hugo Riemann formalisa le Tonnetz (réseau de tons), graphe représentant certaines relations entre notes de musiques (au sens classe de hauteur). De nos jours les théories Néo-Riemanniennes et leurs applications continuent de passionner les mathématico-musiciens. L’originalité du modèle « Planètes 4D », appliqué ici à différents styles de musique, est principalement sa représentation en hyperespace symétrique. Le modèle a été testé à l’aide d’un logiciel interactif avec différents musiciens spécialistes dans leur domaine. Cette article présente l’intérêt et les limites du système expérimental appliqué à différentes variétés de musiques conventionnelles et propose des possibilités d’amélioration du système en fonction des cas étudiés.

Mots-clés : mathématiques – musique – mathématico-musique – Tonnetz – hyperespace – harmonie – visualisation géométrique

Abstract

Sir Isaac Newton was the first to ever study and explain the interaction between light and a glass prism. He connected graphically along his « chromatic circle » colors and music notes. Later, Hugo Riemann formulated the Tonnetz (German word for tone network), a graph displaying particular relations between musical notes described now as « pitch classes ». Nowadays, the Neo-Riemannian theory is still used and researches are performed by mathematico-musicians. The « Planet-4D » model is an original way of representing symmetrically the same pitch space in 4 dimensions. Associated to a piece of software, the system becomes interactive and is tested with different kinds of conventional music: Jazz, Techno, Rap, each variety being performed by a specialist in his field. This paper presents the limits, results and relevance of the system, and proposes some improvements to fit better the requirements of the musicians.

Key-words: mathematics – music – mathematical music – Tonnetz – hyperspace – harmony – geometrical visualization

---

Sommaire 

1. Interactions musico-géométriques
2. Interactions homme-machine
3. Conclusions et perspectives
Notes
Bibliographie

Quel genre d’interactions pouvons-nous imaginer entre des domaines a priori très distincts tels que la physique, la musique, les mathématiques, et l’art ? Tout le monde sait en parler, chacun selon sa propre idée et suivant ses propres expériences. Lors de cette étude nous montrerons quelques aspects originaux concernant des interactions entre les mathématiques et la musique, ainsi que des résultats d’expériences de musique générée en partie par un ordinateur interfacé avec un musicien.

Les relations entre mathématiques et musique sont très étudiées et variées, nous nous intéresserons ici à deux spécialités précises de ces deux domaines : la géométrie (en particulier dans le cas ou un modèle physique peut être représenté) et les classes de hauteurs (ensemble de douze notes ou degrés chromatiques) telles que décrites par exemple dans la set theory d’Allen Forte^1,2 et utilisées par exemple pour la conduite parcimonieuse de voix³. Cet article se place dans ce cadre.

Nous montrerons plusieurs modèles géométriques utilisés qui placent les notes de musique dans des espaces plus ou moins intuitifs et plus ou moins pertinents. Nous présenterons enfin des exemples musicaux d’interactions effectuées entre l’homme et la machine : jouer ou travailler la musique, l’apprendre. Ces exemples ont été crées interactivement avec le logiciel expérimental Planet-Loops, générant un accompagnement musical et visuel selon un parcours harmonique prédéfini ou aléatoire. Le parcours peut être généré par l’ordinateur ou interactivement par le musicien ou un formateur.

1. Interactions musico-géométriques

1. 1. Le cercle de Newton

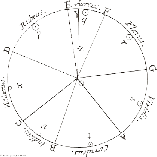
L’interaction de la lumière traversant un prisme et se décomposant en arc-en ciel fascina à l’époque Sir Isaac Newton qui fut le premier à l’étudier et à l’expliquer⁴. Il avait observé que lorsqu’un rayon de lumière solaire pénètre un prisme en verre selon un certain angle, une partie du rayon le traverse et se décompose en bandes colorées.

Il pensait que la lumière était faite de corpuscules de différentes couleurs, et que chaque couleur traversait le prisme à sa propre vitesse. La lumière rouge étant la plus rapide (la violette la plus lente), elle était par conséquent la moins déviée, ce qui créait l’effet spectaculaire du spectre de couleurs. Il choisit sept couleurs : rouge, orange, jaune, vert, bleu, indigo et violet, et y associa les sept notes de musique de la gamme.

À cette époque, il n’était pas encore question de gamme chromatique, ou de théorie moderne plaçant douze notes le long d’un cercle ou dans un espace. La gamme conventionnelle contient sept notes (do, ré, mi, fa, sol, la, si) que l’on peut transcrire avec des lettres (A, B, C, D, E, F, G). La lettre « A » correspondant à la note « La », Newton a de plus disposé les sept notes de la gamme diatonique autour de son illustration, en associant ainsi une couleur à une note, et ordonné les sept notes de façon géométrique : le long d’un cercle.

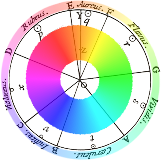
Depuis, la physique moderne nous a apporté d’autres explications concernant la diffraction de la lumière, mais la décomposition de Newton fut pertinente et originale et il fut le premier à associer notes, couleurs, et géométrie. La figure suivante propose une colorisation moderne du cercle original de Newton en ajoutant artificiellement le magenta (qui n’est pas une couleur spectrale). Le cercle noir et blanc, et les annotations d’époques sont présents sur ce dessin.

1. 2. Les Tonnetze

A chaque époque, des théoriciens imaginèrent des illustrations et modèles géométriques décrivant certaines relations privilégiées entre notes ou accords, en général connues des musiciens.

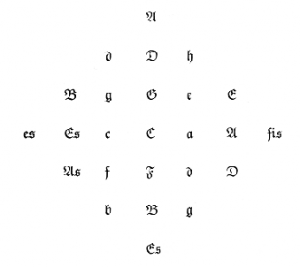
Un Tonnetz, (Tonal Net) traduit de l’allemand par « réseau de tons », est une représentation imaginée par le mathématicien Leonard Euler en 1739. Les premiers Tonnetze furent mis en pratique par le musicologue Hugo Riemann (1849-1919)⁵. Dans un Tonnetz, certaines valeurs de notes sont reliées entre elles ou placées dans les cases adjacentes d’une grille sur un dessin plan. Dans un cadre tonal, tel qu’il fut imaginé à l’origine, le Tonnetz se présentait comme un réseau plan. Depuis, nombre de chercheurs ont considéré ces modèles, et proposé d’autres représentations inspirées de celle d’Hugo Riemann. Ce sont des représentations planes ou tridimensionnelles de ces réseaux, composées de cercles, plans, hexagones, cubes ou tores. Dans le cadre atonal, le Tonnetz se représente habituellement sous la forme d’un Tore 3D, ou d’un graphe dit « Grille-Torique 3×4 »

Au dessin du Tonnetz original d’Hugo Riemann, ont été ajoutées des flèches colorées montrant les intervalles le composant : tierces majeures (rouge), tierces mineures (vert) et quintes (bleu). Les notes seront considérées ici comme classes de hauteur (pitch classes) et représentées dans des espaces de hauteurs (pitch spaces). Lorsqu’il s’agira d’accords, nous parlerons d’espace d’accords (chordal space).

Ainsi le Tonnetz est-il constitué de points : les notes ; et son espace dual formé d’accords à trois sons. Un espace dual se calcule en intervertissant les régions et les points de l’espace. L’espace dual du Tonnetz correspond à la carte des régions de Schoenberg (cf. partie suivante). Le modèle « Planètes 4D » quant à lui, peut être interprété soit comme espace de notes, soit comme espace d’accords selon les besoins et les circonstances.

1. 3. L’espace des accords

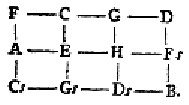
Le théoricien allemand de la musique G. Weber (1779-1839)⁶ représenta graphiquement des relations entre accords majeurs et mineurs à l’aide de ce que nous appelons aujourd’hui en mathématiques un graphe grille.

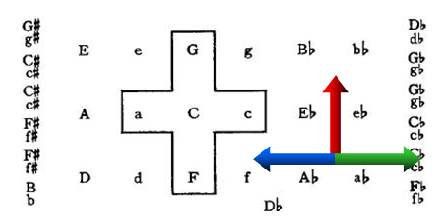
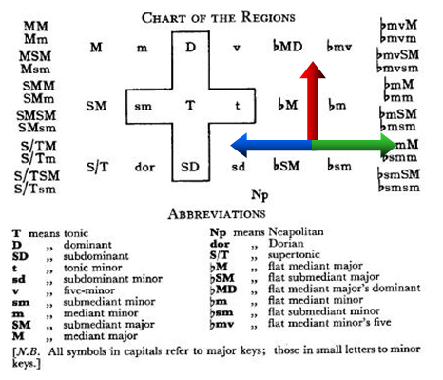
Ce graphe inspira par la suite Arnold Schoenberg (1874-1951) qui créa la carte des régions. La carte des régions de Schoenberg se présentent sous deux formes complémentaires : une forme où les accords sont nommés, ainsi qu’une forme ou les fonctions sont mentionnées.

Dans le premier dessin, Schoenberg représente les accords majeurs et mineurs par leur nom, (C pour Do majeur, A pour La mineur) et n’indique aucune fonction hiérarchique, il y montre seulement le voisinage d’un accord sans y ajouter de sens. C’est un simple placement spatial des accords sur une grille sans volonté, sans hiérarchie ni prévision de parcours harmonique, ni discours. La représentation des accords nommés nous montre simplement tous les chemins possibles, c’est un simple dessin, il n’y a pas de discours.

Par contre, en ce qui concerne la représentation sous forme de fonctions, bien qu’à chaque accord soit associé une fonction harmonique, il n’apparait pas encore de signifiant, il s’agit de signifiance organisée pour produire du sens : un potentiel de production de sens. La Tonique, au centre du schéma, ne prendra sa fonction de Tonique que lorsque qu’elle sera placée dans un schéma global. Il faudra que ses voisins existent pour lui donner sa fonction. Ce schéma présente un discours en activité pas encore achevé.

À l’espace des accords de Schoenberg, ont été ajoutées les flèches colorées montrant les relations harmoniques. En rouge : vers la dominante, en vert : vers l’homonyme, en bleu : vers la relative.

Il est possible de représenter cet espace en 3D, à l’instar de la figure suivante. La notation des accords est celle utilisée par Schoenberg. La variation des couleurs se fait selon le cycle des quintes.

1. 4. Décomposition mathématique de l’espace

Selon des méthodes mathématiques différentes, les théoriciens de la musique ont démontré que l’espace des hauteurs du système tempéré à douze notes peut être considéré comme combinaison de tierces majeures et mineures. Gérard Balzano⁷ montre que ce système « possède la structure d’un groupe cyclique d’ordre douze noté C12, isomorphe au produit de deux de ses sous groupes C3 et C4 ». Thomas Noll⁸ utilise le concept d’un module à douze tons noté T12, et démontre sa décomposition T12=T3⨂T4 avec T3 et T4 étant deux sous-modules de T12 qu’il appelle « cercles externes » (outer circles). Guerino Mazzola⁹ utilise la décomposition de Sylow : Z12=Z3⨂Z4. Gilles Baroin utilise le produit cartésien de deux graphes cycles C3 x C4 pour construire le graphe « Planet Graph » à douze sommets.

Quelque soit la méthode utilisée, chaque note appartient à un seul groupe de trois et un seul groupe de quatre notes, appelés ensemble de tierces majeures et ensemble de tierces mineures.

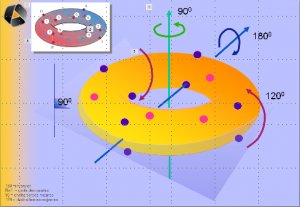
1. 5. Le tore des tierces

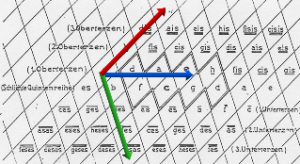
Le tore des tierces est une évocation tridimensionnelle pertinente de l’espace des hauteurs du tempérament égal. Ce modèle qui fut introduit indépendamment par G. Mazzola et G. Balzano¹⁰, est appelé communément le « Tore des Tierces ». Il représente l’espace des hauteurs du tempérament égal et laisse apparaitre les propriétés particulières de la décomposition de l’espace des notes en tierces majeures et tierces mineures. Le Tore des tierces est la représentation moderne du Tonnetz. Il fait apparaitre en trois dimensions les relations présentes dans le Tonnetz original d’Hugo Riemann, ainsi que les symétries suivantes : L’inversion (axe bleu), les rotations de 90° et 120° qui matérialisent les tierces majeures et mineures. Il laisse aussi apparaitre implicitement le cercle des quartes. D’autre visualisations existent mais restent tridimensionnelles¹¹.

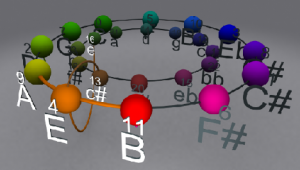
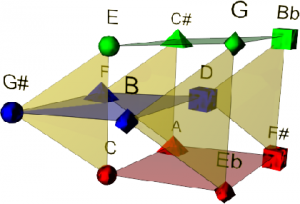
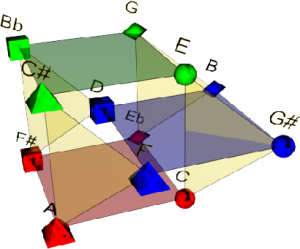
1. 6. Le modèle « Planètes 4D »

Les modèles présentés à ce jour permettent de représenter l’espace des douze notes décomposé en tierces, de façon fonctionnelle et pertinente mais pas totalement symétrique : le tore possède en effet un petit et un grand rayon ! Afin que chaque tierce soit de même longueur géométrique dans un modèle physique, le modèle devra se situer en hyperespace : ici de dimension quatre.

La recherche du modèle Planet, sa représentation et ses applications sont détaillée dans ma thèse. En partant de conditions d’hyper-symétrie inspirées du théorème de Nöther, nous avons montré au cours d’un raisonnement déductif, illustré d’exemples musicaux, que l’ensemble des 12 classes de hauteurs peut se représenter pertinemment par un graphe dit « graphe Planètes ». Ce graphe se caractérise parmi les graphes abéliens de Cayley et nous en avons détaillé les propriétés remarquables.

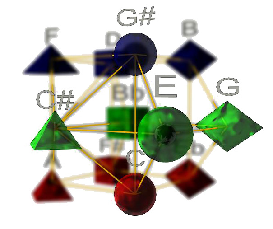
NB : Le modèle n’est pas seulement géométrique, il comporte aussi des symétries sémiotiques : les idéogrammes bi-dimensionnels (forme et couleur) utilisés pour la représentation font partie du modèle. Le modèle est composé de carrés et triangles, chaque sommet est à l’intersection d’un carré et d’un triangle. Nous avons associé chacun des paramètres de la décomposition de l’espace des hauteurs à un paramètre de l’idéogramme représentant cette note. De ceci résulte 12 idéogrammes bidimensionnels composés de quatre formes et trois couleurs différentes.

Le modèle Planet peut s’interpréter de deux façons différentes, statiquement en temps qu’espace de hauteurs comme un Tonnetz, ou dynamiquement en temps qu’espace d’accords. L’interprétation statique est une représentation des classes de hauteurs dans un espace géométrique, nous y remarquerons les propriétés des symétries calculées ainsi que les relations entre notes grâce au système de formes et de couleurs.

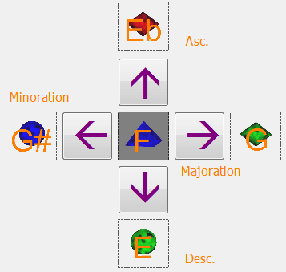
Lors de l’interprétation dynamique, nous nous déplacerons virtuellement d’un point à un autre du modèle, en générant en chaque endroit une note ou un accord (au sens large du terme), ayant pour base cette note. Les déplacements à l’intérieur du modèle sont des propositions de modulation qui peuvent être suivies par un Jazzman travaillant ses gammes ou un groupe de musicien relevant le défi de suivre un parcours harmonique aléatoire et symétrique.

Le modèle 4D fait apparaitre de façon native les relations entre tierces et de façon sous-jacente les cercles des quartes / quintes et cercles chromatiques.

La visualisation d’un modèle 4D n’étant pas aisée avec un support tel que cet article, des représentations vidéo en 3D et 4D sont disponibles sur ce site.

2. Interactions homme-machine

2. 1. Logiciel interactif

Le logiciel interactif « Planet-Loops » a été développé dans le but de montrer acoustiquement les possibilités d’utilisation du modèle Planet et de tester ses limites dans plusieurs environnements expérimentaux. « Planet-Loops » peut être paramétré pour se déplacer dans différents systèmes de représentation ou placement d’accords. Il peut s’adapter par exemple à des parcours entre trois accords de Blues, le long d’un Tonnetz ou selon des règles paramétrables prédéfinies. Dans cette étude nous montrerons essentiellement son utilisation avec le système « Planet 4D » décrit précédemment et qui comporte exclusivement les relations de tierces majeures et mineures. Le système mathématique symétrique est à l’origine du modèle devant conduire à un environnement musical en espace clos, lui-même symétrique.

Nous nous plaçons dans un cadre de parcours de modulations, les sommets du modèle étant considérés comme des accords ou des tonalités de base. L’accord est considéré ici au sens d’un « accord de grille » tel que dans le Jazz ou le Rock, accord d’accompagnement joué par exemple par le guitariste. Comme ce logiciel se situe dans un cadre général, nous utiliserons les termes style, genre, rythme, mélodie dans leur sens généralement compris par un large public mélomane et non spécialiste de musicologie.

Le logiciel est un arrangeur comportant les sections habituelles au monde des claviers arrangeurs (ex : Yamaha PSR) : l’accompagnement et la mélodie. Les utilisateurs de claviers arrangeurs sont souvent des musiciens amateurs qui utilisent les possibilités de l’accompagnement automatique pour créer leurs premières compositions ou s’accompagner au chant sans avoir à utiliser un ordinateur avec un séquenceur qui demande une prise en main plus difficile. Les « Live-Stylers »sont des pianistes de bar professionnels des temps modernes qui chantent en s’accompagnant interactivement avec un clavier arrangeur haut de gamme. Ils proposent ainsi une solution intermédiaire entre le petit orchestre et la bande enregistrée qui ne permet aucune interaction avec les réactions du public. Comme avec un clavier ordinaire, dans notre logiciel, l’artiste sélectionne un style prédéfini (Jazz, Techno, Rock, Blues, …), utilise les variations de style programmées, ajoute une mélodie et choisit un accord de base. Le logiciel étant expérimental, il n’a pas prétention à rivaliser avec du matériel professionnel, mais présente des possibilités en vue de développements futurs.

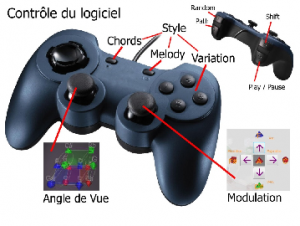
L’originalité de l’interaction réside principalement dans le fait que l’utilisateur peut interférer avec la production musicale en cours par l’intermédiaire d’un Joystick ou de toute autre interface configurée pour le PC. L’interface est employée pour modifier le style d’accompagnement, la mélodie en cours, et définir l’accord utilisé. Le joystick présente un caractère ludique qui rassure le musicien amateur n’ayant pas envie ou besoin de connaitre les notes et accords et qui désire quand même suivre un Blues ou une autre grille. Les déplacements dans l’espace d’accords permettent à l’utilisateur de visualiser et d’entendre les modulations simultanément.

Il est bien sûr possible d’interfacer le logiciel avec un vrai clavier électronique. Chaque style contient plusieurs motifs pour l’accompagnement et pour la mélodie. Le fichier Jazz contient par exemple six accompagnements rythmiques différents (drums, bass, piano et combinaisons). Une section d’accompagnement comporte jusqu’à huit motifs différents que l’ordinateur module et joue dans la tonalité choisie par le musicien. Il s’agit bien de modulations et non de transpositions, la forme de l’accord (son renversement) variant afin d’éviter un changement trop brutal entre deux tonalités. La section mélodique produira des phrases ou ensembles de phrases jouées par les instruments, toujours dans la tonalité choisie.

Le logiciel produit une boucle musicale dans la tonalité choisie, et propose des possibilités de modulation. Le choix du prochain accord peut être décidé par l’ordinateur ou laissé à l’initiative du musicien ou d’un tiers qui montre le parcours à suivre. Il s’agit en résumé d’une machine à moduler couplée à un arrangeur basique contrôlable sans aucune connaissance du solfège.

L’interface visuelle du logiciel comporte : à gauche une représentation de la position actuelle en 4D, à droite une représentation plane montrant les quatre directions possibles de modulation.

2. 2. L’expérience du jazz

Pour l’expérience Jazz, nous avons travaillé avec des enchaînements d’accords, et une rythmique inspirée de So What de Miles Davis. Ce morceau est typique du Jazz modal, la grille comporte 8 mesures de Ré mineur ( noté D-, parfois appelé Ré dorien) suivies de 8 mesures de Mib mineur (Eb-). En suivant le modèle « Planet », il y a par conséquent en chaque point quatre possibilités de modulation correspondant aux quatre accords mineurs ayant une note commune avec l’accord en cours. Exemple : si nous sommes en Do-, les quatre possibilités seront La-, Mib-, Lab- et Mi-. Le fait d’utiliser des accords mineurs sans relation fonctionnelle entre eux nous place bien dans un cadre de Jazz Modal. La différence primordiale avec une session traditionnelle est que le musicien ne connait pas la grille par avance et ne calcule ses enchainements qu’au dernier instant.

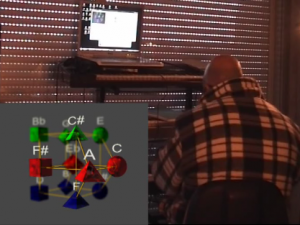
Le système à été testé avec un pianiste professionnel expérimenté qui a pris plaisir à l’expérience inhabituelle de découvrir visuellement le prochain accord à la volée.

Au contraire du rappeur qui a besoin de stabilité harmonique, le musicien de jazz aime les modulations et tire une partie de son plaisir à improviser en suivant une grille d’accords changeants. Le Jazzman est habitué à suivre une grille ou un ensemble de musiciens à l’oreille, il est très sensible à l’harmonie. Dans le cas présent, le pianiste jouait une partie d’accompagnement composée d’accords à la main gauche et une partie solo à la main droite. L’improvisation s’est déroulée en deux temps. Pour l’introduction du morceau, l’ordinateur marquait le tempo avec pour seul instrument le Charley (Cymbale fermée) tout en affichant à l’écran le parcours harmonique proposé, le pianiste improvisait en suivant la grille dynamique. Une fois le musicien décidé, et à sa demande, le logiciel à ajouté une ligne de basse ainsi qu’une batterie plus complète, en vue de simuler le contexte du trio ou le pianiste joue des accords adaptés à gauche et un chorus à droite.

Dans cette expérience, c’est l’ordinateur qui décidait quasi-aléatoirement du parcours d’accords. La règle étant de passer par les douze sommets du modèle une fois et une seule (ceci correspond en théorie des graphes au chemin Hamiltonien). Il est pratiquement improbable que le musicien puisse deviner le prochain accord parmi les quatre possibilités. Chaque séquence durant quatre mesures (à tempo 140) la proposition apparaissait à l’écran au début de la dernière mesure, soit moins de deux secondes avant le changement d’accord. Le pianiste avait assez de temps pour penser l’enchaînement à venir, et le préparer. Le résultat donne un Jazz dans le style souhaité mais qui ne comporte pas de fonction tonale ou de discours, à contrario de So What ou le morceau à été composé, possède une structure, commence et termine dans la même tonalité.

Dans un deuxième temps, nous avons augmenté progressivement la fréquence de changement entre les modulations, forçant ainsi le musicien à un effort de calcul de plus en plus grand. Dans le cas présent nous avons constaté qu’une fréquence de changement d’accords de deux par mesure 4/4 à Tempo 140 était la limite supérieure pour cet exercice, des fréquences plus grandes n’apportant plus le même plaisir au musicien. Giant Steps, composé et interprété par John Coltrane, est un morceau réputé difficile à jouer, où les accords s’enchainent aussi selon des tierces et bien plus rapidement, mais la grille est connue d’avance.

L’outil permet ainsi de tester les capacités et la vitesse d’adaptation du musicien. Afin de l’améliorer pour le Jazz il faudra l’utiliser avec une plus grande variété d’accords fondamentaux, de types de parcours, et envisager une interface montrant les deux accords suivants prévus par l’ordinateur ou un instructeur.

2. 3. L’expérience du rap

Dans le style de Rap testé ici, le motif de la boucle rythmique varie peu, celle-ci est composée d’une séquence répétitive d’accords qui s’enchainent tout au long des couplets et refrains. La réalisation est instrumentalement proche du style Gangsta-Rap popularisé par Dr.Dre. Avec le logiciel « Planet-Loops », nous considérons les sommets du modèle comme des tonalités de base dans lesquelles sera modulée la phrase musicale répétitive. Il s’agit donc, dans ce cas particulier, de vraies modulations au sens tonal du terme. Chaque phrase musicale ayant déjà sa propre structure harmonique. L’exemple montré ici utilise les suites d’accords suivantes : {Cm6, B7, Dm, A} pour l’introduction et {Cm, Fm, G, Cm} pour le refrain et le couplet, où la rythmique et l’orchestration diffèrent, mais la suite d’accords reste la même. Ces suites d’accords seront modulées en direct par le chanteur à l’aide du joystick, selon son appréciation. Il en ressort que, malgré le son synthétique généré par l’ordinateur, le ressenti est agréable et inhabituel pour le chanteur et l’auditeur.

Le Rap ne module pas en général, on rencontre parfois une ou deux modulations au cours d’un titre, celles-ci s’appliquant au refrain qui est repris dans une tonalité généralement un demi-ton ou un ton plus haut. Il n’est pas très aisé pour un chanteur de suivre les modulations si elles s’enchainent trop rapidement, le rappeur se concentre habituellement sur son phrasé et le rythme, l’harmonie étant une composante annexe pour ce type de musique.

Après plusieurs tentatives d’adaptation, il a été remarqué que les modulations ne doivent pas intervenir plus fréquemment que toutes les deux ou quatre mesures (à tempo 90) afin de laisser au chanteur le temps de s’adapter. Les tonalités de base différant d’une tierce entre chaque, le passage n’est pas très abrupt et le chanteur s’adapte facilement. Il est à noter que même si le rappeur déclame un texte très accentué rythmiquement, sans mélodie vraiment perceptible et proche de la parole, l’auditeur ressent toutefois l’effet des modulations dans son chant. La production enregistrée et présentée lors de la conférence est disponible sur ce site. Afin d’améliorer le système pour le Rap, il faudra utiliser des sons plus modernes et des boucles plus réalistes.

2. 4. L’expérience de la techno

Les effets de modulation sont extrêmement rares voir absents de la musique techno. Certains parmi les musiciens techno ne connaissent pas le solfège, en ont peur par principe, ou bien n’en ont pas besoin pour exercer. D’apparence facile et très répétitive, la musique techno est éloignée de la musique classique, elle requiert des connaissances et aptitudes différentes. Les musiciens opérant derrière leurs platines trouvent leur intérêt dans la maitrise du son et l’interaction avec le public dansant pendant de très longues heures. Si elle ne module pas, la boucle principale change très fréquemment et varie selon des paramètres autres que l’harmonie ou la mélodie. Par exemple le timbre, le placement spatial, le mélange avec des bruitages ou le tempo. L’utilisation de filtres passe-haut et passe-bas associés aux modifications de hauteur sont très usités et s’opèrent manuellement durant la performance. Ce sont à la fois le caractère répétitif de cette musique et ses variations dans la continuité qui en font l’intérêt et amènent le danseur à des états de transe. Le DJ préfère se designer par le terme « liveur » (liver) car il ne passe pas seulement des disques en soirée mais crée sa musique en direct avec ses boites à rythmes et échantillonneurs (grooveboxes et samplers). Il mélange en direct divers instruments rythmiques provenant de boucles et un minimum de mélodie en jouant avec les effets. Le logiciel permet de changer la rythmique en direct beaucoup moins facilement qu’avec le matériel habituel (table de mixage, et générateurs de boucles), mais il fut toutefois suffisant pour une première expérience. En général les modulations utilisées en Techno se limitent à parcourir en boucle deux accords proches (par exemple Am, A). Nous avons utilisé pour cet exemple huit types de rythmiques qui ne modulent pas (Bass Drum, Kick, Charley) et six types de mélodies modulantes (Bass, Melody…) Les mélodies utilisées dans ce cadre ne comportent que peu de notes et les variations sont surtout présentes dans le timbre. Les lignes de basse ont été comptées parmi les mélodies. À cette heure, le logiciel ne gère pas les effets d’accélération et de ralenti utilisés en techno, ce qui n’est pas déterminant car les tests ont été effectués avec moins d’échantillons que pour un morceau habituel, et pour des durées de titre courtes, de l’ordre de 3 minutes.

Les tests ont été effectués avec un DJ compositeur, liver et producteur de musique techno, ne connaissant pas le solfège, habitué à travailler avec des logiciels et du matériel de commerce. Il en est ressorti que l’effet de modulation dans cette musique apportait des sensations nouvelles au DJ qui essayait le parcours harmonique comme un nouveau jouet et en appréciait les effets sans avoir besoin d’en connaitre le fondement. L’orchestration est très rudimentaire , les modulations à la tierce enchainées à la suite donnent une impression de progression cyclique sans fin, et ajoutent une touche inhabituelle à cette musique tout en renforçant l’impression de variation dans la continuité, et sans modifier la composante rythmique essentielle à ce style.

D’autre part, une production non interactive Peplum feat le Baron a été conçue indépendamment de l’expérience décrite précédemment en programmant au préalable une suite d’accords selon un chemin issu du modèle « Planet » dans le séquenceur habituel du musicien. Ce dernier a pu alors mixer en direct la séquence en utilisant sa table, ses filtres et ses effets familiers. Dans ce cas où le modèle ne pouvait pas être techniquement interactif, les effets de modulations étaient sensibles bien que non décidés par l’interprète.

Afin de perfectionner le système pour la techno, il faudra l’interfacer avec du matériel existant dans le but d’utiliser les effets de tempo, spatialisation et variation des fréquences en direct et modifier la commande depuis le joystick afin de pouvoir superposer des boucles prédéfinies.

2. 5. L’expérience de l’orgue

L’orgue de la cathédrale de Saint-Lizier est un instrument récemment restauré dans sa composition d’origine du XVIIe siècle. Le modèle « Planet » ainsi que les Tonnetze construits à partir du tempérament égal ne fonctionnent pas en théorie avec le tempérament inégal de l’orgue.

La pratique l’a confirmé. Cependant, les tests effectués avec l’orgue ont été probants dans la mesure où la musique produite correspondait au résultat attendu et « dérangeait l’oreille » dans certaines tonalités. En effet, un orgue de cathédrale n’est pas accordé au tempérament égal, tel un piano actuel (en théorie), car cette organisation de sons n’existait pas à l’époque de sa conception. L’orgue privilégie naturellement les tonalités pour lesquelles il a été conçu et est parfaitement adapté à la musique de son époque. Notons que le célèbre « clavier bien tempéré » de J.S Bach n’est pas d’un tempérament égal où tous les écarts chromatiques sont identiques. Il permet, par contre, de jouer juste dans chaque tonalité, avec une couleur différente, ce qui n’est pas le cas avec l’instrument de la cathédrale. L’improvisation s’est déroulée à deux mains et au pédalier en jouant plutôt lentement afin de ressentir les effets souhaités sans saturer l’espace acoustique (la réverbération était importante). Le logiciel ne générait pas d’accompagnement sonore mais montrait seulement un chemin passant par les sommets du modèle. Seuls les accords voisins (au sens théorique du terme = différant de peu d’altérations) de la tonalité de base de l’orgue sonnaient effectivement juste.

Le fait de se déplacer de tierce en tierce créait une impression très inhabituelle, plutôt dérangeante alternant le juste et le faux, témoignant ainsi acoustiquement que le système « Planet » ne fonctionne pas avec un tempérament inégal. Ceci s’entend, bien sûr, pour une oreille ordinaire habituée à la plupart de notre musique conventionnelle.

2 6. Musique d’ambiance électro

La musique d’ambiance à base électronique s’adapte assez bien au logiciel et au système. Nous avons testé ses effets avec différentes combinaisons de parties rythmiques et mélodiques en restant dans une atmosphère planante et sans rythmique excessive. Dans ce genre de musique, il est aisé de créer des boucles avec une instrumentation changeante et évoluant sans grande discontinuité. Les sons proviennent de synthétiseurs pour les nappes et instruments solo, et de boucles rythmiques (drum loops) préenregistrées pour la base de la partie accompagnante. En combinant huit types de boucles pour l’accompagnement, et huit types pour la mélodie, nous avons pu ainsi créer les impressions acoustiques différentes qui pourraient accompagner des images et être utilisées par exemple, pour la production automatique de musique d’ambiance libre de droits. Après avoir géré manuellement les passages d’accords en faisant varier très peu l’accompagnement afin de mieux ressentir les effets des modulations, il a été constaté que les modulations donnaient des effets assez similaires. Le choix des déplacements harmoniques a donc été laissé à l’ordinateur qui a généré de façon aléatoire et en direct le parcours harmonique, l’utilisateur ne jouant qu’avec les paramètres de l’orchestration : accompagnement et mélodies. L’utilisateur qui n’agit que sur les paramètres de l’orchestration n’est aucunement gêné par les modulations automatiques qui apportent à ce genre de musique la sensation recherchée d’univers clos et de progression infinie. La musique d’ambiance produite à été utilisée en association avec des peintures numériques dynamiques, utilisant aussi les principes de symétrie et répétitions à l’infini^12,13.

3. Conclusions et perspectives

Le modèle « Planet 4D » s’inscrit certes dans la lignée des Tonnetze existants décrivant l’espace des hauteurs, mais il apporte de nouvelles visualisations et une sensation de vraie symétrie visuelle que seule une sphère possède. Les idéogrammes représentant des notes voisines ne diffèrent que d’un paramètre : forme ou couleur, le système idéographique original à deux dimensions renforce la sensation d’invariance. Le logiciel interactif expérimental développé pour tester le modèle de façon dynamique fonctionne et donne des résultats conformes en ce qui concerne les musiques conventionnelles testées, dans le cadre des chemins symétriques. Le modèle montre ses limites comme par exemple dans le cas de tests avec un orgue de cathédrale. Le logiciel sera amélioré afin de mieux répondre aux différents besoins des diverses catégories d’utilisateurs. Le modèle « Planet 4D » est à la base un espace de hauteurs, il est utilisé aussi dynamiquement comme espace d’accords, chaque accord étant de même type : mineur – majeur. Il est prévu de réaliser un modèle 4D représentant le Tonnetz avec ses douze notes et les vingt-quatre accords à trois sons, toujours de façon symétrique en hyperespace. Dans ce cas nous pourrons utiliser dynamiquement le modèle pour visualiser la technique conduite de parcimonie de voix sur une hypersphère. Ce modèle plus complet permettra de nouvelles visualisations géométriques de l’harmonie contenue dans des œuvres existantes.

---

Notes